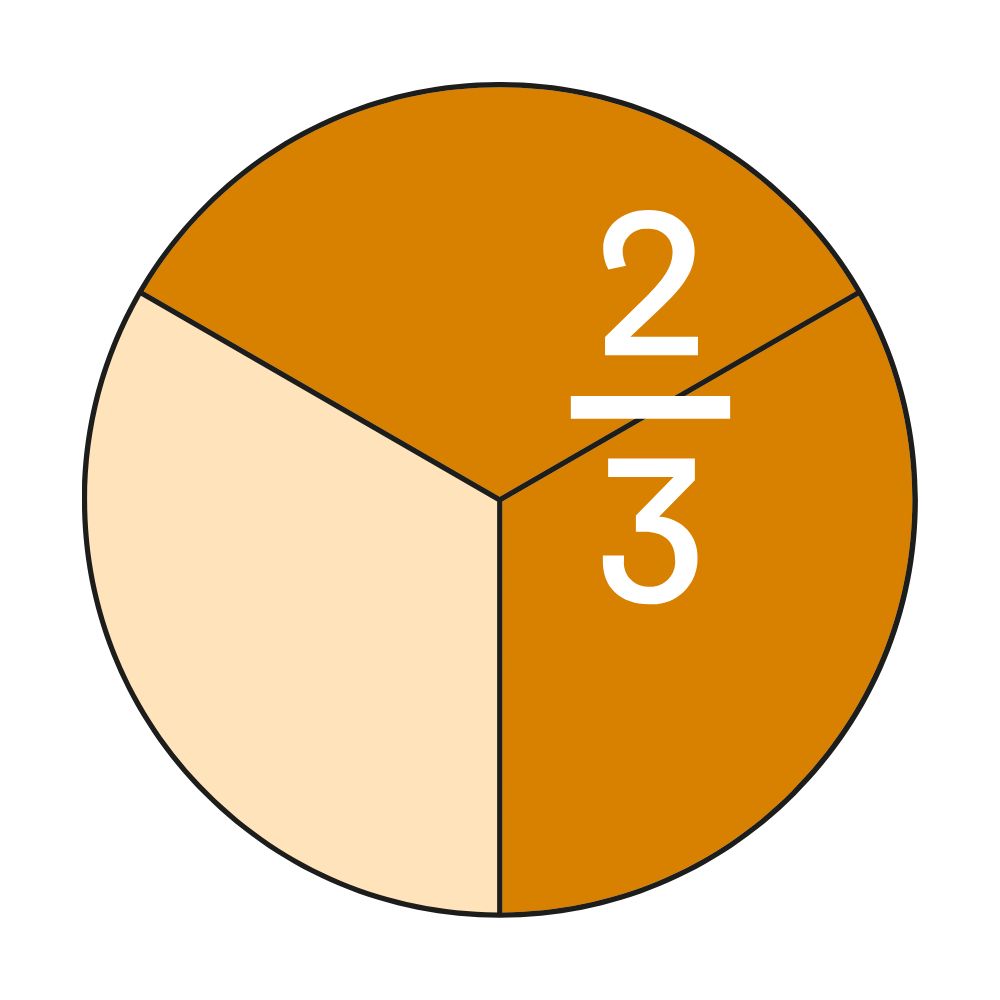
Ile to jest 2/3? Odkrywanie tajemnic ułamków
Ułamki,choć mogą wydawać się skomplikowane i abstrakcyjne,są nieodłącznym elementem naszego codziennego życia. Spotykamy się z nimi w kuchni, przy zakupach, a nawet w czasie planowania wypoczynku. Jednym z często pojawiających się pytań jest: „Ile to jest 2/3?” Paradoksalnie,odpowiedź na to pytanie otwiera przed nami świat matematycznych konceptów,zmuszając do refleksji nad tym,jak liczby wpływają na nasze postrzeganie rzeczywistości. W tej artykule przyjrzymy się nie tylko wynikom obliczeń, ale i praktycznym zastosowaniom ułamków w życiu codziennym. Czy jesteście gotowi na matematyczną podróż, która pomoże zrozumieć wartość 2/3 w bardziej przystępny sposób? Zapraszam do zgłębienia tego fascynującego tematu!
Zrozumienie ułamków – co oznacza 2/3 w praktyce
Ułamki to nie tylko matematyczne pojęcia, ale także narzędzia, które pomagają zrozumieć i opisać otaczający nas świat. Kiedy mówimy o 2/3,mamy do czynienia z częścią całości. W praktyce oznacza to, że z trzech równych części weźmiemy dwie. Może to być zastosowane w różnych sytuacjach, od kulinarnych przepisów po dzielenie się zasobami.
Aby lepiej zrozumieć, co oznacza ta liczba w praktyce, warto przyjrzeć się przykładom. Wyobraźmy sobie, że pieczemy ciasto, które wymaga 3 szklanek mąki. Jeśli zdecydujemy się użyć 2/3 tej ilości, będziemy potrzebować:
| Składnik | Ilość |
|---|---|
| Mąka | 2 szklanki |
| Cukier | 1 szklanka |
W innym przypadku, 2/3 może odnosić się do dzielenia. Na przykład,jeśli mamy 6 jabłek i chcemy podzielić się nimi z przyjaciółmi,weźmiemy 4 jabłka jako 2/3 całości. Można to zobaczyć jako:
- 6 jabłek w całości
- 2/3 z 6 = 4 jabłka
Jak widać, ułamki, takie jak 2/3, mają kluczowe znaczenie w codziennym życiu. pomagają nam w lepszym zarządzaniu zasobami, oszczędzaniu czasu w kuchni i w wykonywaniu wielu innych czynności, które wymagają podziału. Im lepiej zrozumiemy ich mechanikę, tym sprawniej będziemy mogli z nich korzystać.
Przykłady zastosowania 2/3 w codziennym życiu
W codziennym życiu spotykamy się z pojęciem ułamków w wielu różnych sytuacjach. Przykładem może być przygotowanie posiłków, gdzie często musimy podzielić składniki w odpowiednich proporcjach. Gdy przepis wymaga 2/3 szklanki cukru, łatwo zrozumieć, że to oznacza, że powinniśmy użyć dwóch pełnych łyżek oraz jednej dodatkowej łyżki. Dzięki temu zapewniamy idealny smak i konsystencję dania.
Innym zastosowaniem 2/3 może być planowanie budżetu domowego. Jeśli mamy miesięczny dochód wynoszący 3000 zł, a chcemy przeznaczyć na oszczędności 2/3 tej kwoty, to oznacza, że na oszczędności powinniśmy odkładać 2000 zł. W taki sposób możemy łatwo kontrolować nasze wydatki oraz mieć możliwość realizacji większych celów finansowych.
Warto również zwrócić uwagę na aspekt zdrowotny.Na przykład, w diecie często zaleca się podział talerza na różne składniki.Jeśli chcemy, by 2/3 naszego talerza były wypełnione warzywami, a pozostała część białkiem, to również jest to praktyczne zastosowanie ułamków. Pomaga to w lepszym bilansowaniu diety i dbaniu o zdrowie.
| Przykład Zastosowania | Konkretny Ułamek | Opis |
|---|---|---|
| Gotowanie | 2/3 szklanki | Cukru do wypieków |
| Budżet | 2/3 dochodu | Kwota przeznaczona na oszczędności |
| Dieta | 2/3 talerza | Warzywa jako główny składnik posiłku |
Jak obliczyć 2/3 w różnych kontekstach matematycznych
Obliczanie ułamków, takich jak 2/3, może być przydatne w różnych sytuacjach, zarówno w matematyce czystej, jak i praktycznej. W kontekście prostych działań arytmetycznych, 2/3 można interpretować jako proporcję. Gdy mamy łącznie 3 równe części, 2/3 oznacza, że wybieramy 2 z tych 3 części. Przykładowo, jeśli masz 3 jabłka i chcesz obliczyć, ile to będzie 2/3 z tej ilości, to otrzymasz 2 jabłka. Można to wizualizować w prosty sposób, korzystając z diagramów kołowych:
| Całkowita liczba części | Wybrane części (2/3) |
|---|---|
| 3 części | 2 części |
W kontekście geometrii, 2/3 może odnosić się do obliczeń powierzchni lub objętości. Jeśli mamy kawałek doskonałej formy, takiej jak sześcian, to możemy obliczyć 2/3 jego objętości. Dla sześcianu o krawędzi 3 cm (objętość = 3^3 = 27 cm³), 2/3 objętości sześcianu wyniesie:
V = (2/3) * 27 cm³ = 18 cm³
W zastosowaniach codziennych, obliczanie 2/3 jest niezwykle praktyczne. Może się to przydać przy dzieleniu jedzenia, przy zakupach lub podczas planowania rafinowanych przepisów kulinarnych. Na przykład, jeśli przepis wymaga 3 szklanek mleka, a ty chcesz przygotować tylko 2/3 przepisu, wystarczy obliczyć, ile to będzie:
- 3 szklanki * (2/3) = 2 szklanki mleka
Tak więc, w różnych kontekstach, 2/3 przyjmuje formę ułamka, który jest elastyczny i niezwykle użyteczny w praktycznych zastosowaniach matematycznych oraz codziennym życiu.
Rekomendacje dotyczące nauki i nauczania ułamków
W procesie nauki o ułamkach kluczowe jest zrozumienie ich zastosowań w codziennym życiu oraz umiejętność wizualizacji tych wartości. Ułamki, takie jak 2/3, można łatwo przedstawić za pomocą różnych modeli, co może ułatwić zrozumienie uczniom. Oto kilka rekomendacji, które mogą przynieść efekty w nauczaniu tej tematyki:
- Wizualizacje: Używanie rysunków, modeli czy wykresów, które przedstawiają ułamki jako części całości, jest bardzo pomocne. Można na przykład przedstawić 2/3 jako dwa z trzech równych kawałków na torcie.
- Przykłady z życia codziennego: Zastosowanie ułamków w kontekście, na przykład przy dzieleniu jedzenia, może pokazać uczniom, jak często stosujemy te wartości.Uczniowie mogą na żywo doświadczać podziałów, co ułatwi ich zrozumienie.
- Gry edukacyjne: Wprowadzenie elementów zabawy, takich jak gry planszowe czy aplikacje, które angażują uczniów i pozwalają na praktyczne ćwiczenie ułamków, może znacząco zwiększyć zainteresowanie tematem.
Warto również wprowadzać ćwiczenia, które będą stopniowo zwiększać rozwój umiejętności uczniów. Możesz na przykład stworzyć prostą tabelę, która pomoże im zrozumieć, jak dzielą się różne ułamki:
| Ułamek | Przykład wizualizacji | Opis |
|---|---|---|
| 1/2 | 🍰 | Połowa ciasta |
| 2/3 | 🍰🍰 | dwa kawałki z trzech |
| 3/4 | 🍰🍰🍰 | Trzy kawałki z czterech |
Takie działania nie tylko wzbogacają proces nauki, ale także sprawiają, że staje się on bardziej ciekawy i angażujący dla uczniów. pamiętaj, że kluczem do sukcesu jest cierpliwość oraz elastyczność w podejściu do nauczania.
Podsumowując
Podsumowując, zagadnienie dotyczące wartości ułamka 2/3 nie tylko ułatwia nam codzienne obliczenia, ale także otwiera drzwi do głębszego zrozumienia matematyki i jej zastosowań w życiu codziennym.Choć na pierwszy rzut oka może wydawać się proste, zasady rządzące ułamkami skrywają wiele możliwości, które możemy wykorzystać w praktyce. Pamiętajmy, że matematyka nie jest jedynie zestawem formuł, lecz narzędziem, które pozwala nam lepiej zrozumieć świat wokół nas. Warto zgłębiać te tajniki, poszerzając swoje umiejętności oraz pewność siebie w obliczeniach. Dziękujemy za towarzyszenie nam w tej podróży po fascynującym świecie ułamków!